Analyse du phénomène d'attente dans un club sportif : Système d'attente avec un seul serveur qui traite toujours deux clients à la fois et où un des clients peut demander à nouveau d'être servi
On considère un petit club (de tennis ou de squash, par exemple) qui ne possède qu'un seul court. S'il n'y a pas de membre dans le club ou s'il n'y a qu'un seul membre dans le club, aucune partie ne peut être organisée. Dès l'instant où il y a au moins deux joueurs dans le club, un match démarre. A l'issue de ce match, le perdant quitte le club, alors que le gagnant a le choix : ou bien il part, ou bien il reste et joue avec un joueur de la file d'attente. Il peut décider de partir même s'il n'y a qu'un seul joueur à attendre et celui-ci devra attendre l'arrivée d'un autre joueur (et il va attendre car il s'est déplacé et veut jouer au minimum une partie)..
On accepte les hypothèses (réalistes) suivantes : les membres du club arrivent pour jouer selon une loi de poisson de paramètre
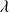(probabilité
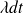d'une arrivée sur l'intervalle
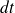), la loi de durée des matchs est exponentielle (probabilité
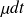d'une fin de match sur l'intervalle dt si un match est en cours),
est la probabilité que le gagnant n'ait pas envie de continuer de jouer et
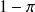qu'il décide de rester.
Questions
On vous demande de dessiner le graphe associé à la chaîne de Markov décrivant le système d'attente du club sportif. Chaque sommet du graphe correspond à un état dénoté par
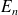où n est le nombre de joueurs présents dans le club. On néglige les probabilités en
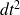, on ne vous demande pas de représenter les boucles et vous avez le droit de diviser les probabilités de transition par
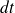. On suppose dans cette question que
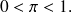
On étudie maintenant les cas particuliers où
π=0,
π=1,
en négligeant toujours les probabilités en
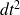, dessiner les chaînes de Markov correspondantes et préciser si, dans ces deux cas particuliers, le système d'attente est un phénomène de naissance et de mort (ou s'il le devient rapidement) en justifiant votre réponse.
