Une réunion perturbée
Dans une salle sont réunies N V.I.P. (Very Important Persons). Les points importants ne peuvent être examinés et les votes ne peuvent avoir lieu que si les N personnes sont simultanément présentes dans la salle. Mais, comme elles ne peuvent se passer de contacts téléphoniques fréquents avec leur empire industriel et que les lieux ne permettent pas d'utiliser les téléphones portables, deux postes téléphoniques ont été installés dans deux bureaux voisins et les personnes quittent la salle pour répondre, lorsqu'elles sont appelées sur une des deux lignes (non occupées par une autre personne).
Pour chaque personne, la loi des arrivées des appels téléphoniques est une loi de poisson dont le taux inter-arrivées est de
.
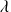Le taux de service correspondant aux réponses téléphoniques est de
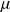, la longueur des conversations téléphoniques étant supposée suivre une loi exponentielle.
(On suppose comme d'habitude que la probabilité de deux appels simultanés ou de deux fins de communication simultanées ou d'une fin de communication simultanée à un appel est totalement négligeable).
Questions
Quels sont les états et le graphe de transition de ce phénomène d'attente?
Quelles sont les équations du régime permanent?
Quelle est la probabilité
en régime permanent de l'état "on peut discuter et prendre des décisions car tout le monde est là"? (l'exprimer en fonction de N et de
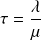)Pour l'application numérique, vous avez le choix entre:
calculer simplement la probabilité
pour N=5 et τ=0,1 et 0,5.calculer la valeur maximale que peut prendre le ratio
pour que la probabilité
soit supérieure ou égale à 0,5 pour N=2, 3, 4 et 5.
