Correction Question 2
Partie 1
Il faut d'abord considérer que la sous-matrice Q correspond aux C0, C1, C2 (ce qui était évident puisque l'on donnait les états associés à la matrice fondamentale N).
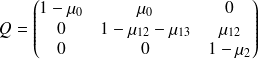
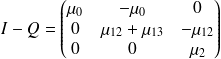
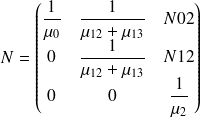
Et on a (I-Q).N qui doit être égal à la matrice identité.
En notant N02 et N12 les coefficients manquant dans la matrice N, et en posant (I-Q).N=I on obtient les équations :
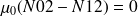
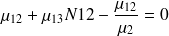
On en déduit :
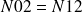 et
et
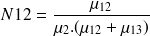
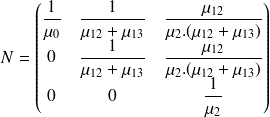
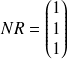
La matrice N.R ne contient que des 1. Ce résultat est normal, puisque quelque soit l'état transient (ou transitoire) dont on part, on termine obligatoirement en classe 3.





