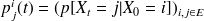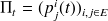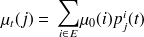Représentation matricielle
Soit E un espace d'état fini. Une mesure de probabilité sur E est déterminée par les valeurs
.
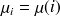On le repérera par le vecteur ligne que l'on notera
.
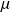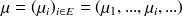
Une fonction
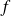sera représentée par le vecteur colonne noté encore :
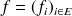où
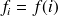
On aura alors
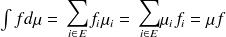
Représentation des probabilités conditionnelles par une matrice
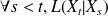est une famille de lois de probabilité. Le fait que l'on suppose l'espace d'état fini nous permet d'adopter un formalisme matriciel simple. En effet, si on remarque que
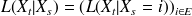, puisque cela définit bien la loi sur tout l'espace d'état, et que l'on prend pour convention que
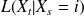est représenté par un vecteur ligne on peut alors représenter complètement
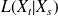par la matrice
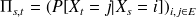
Donc
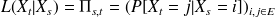
i : indice de la ligne
j : indice de la colonne
Si on note
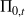par
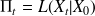, alors dans ce cas, l'homogénéité se traduit par :
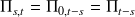
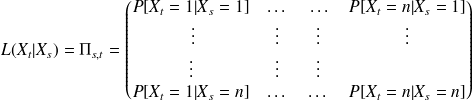
D'autre part, si on connait la loi
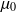de
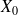, alors la loi de
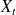notée
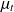sera égale à
On écrit :
