Équivalence sur C
Méthode :
Soit
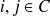 , alors tous les éléments de
, alors tous les éléments de
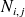 ont même reste dans la division par d.
ont même reste dans la division par d.
C'est à dire :
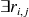 tel que
tel que
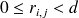 ,
,
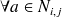 ,
,
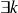 tel que :
tel que :
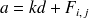
Méthode :
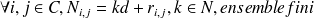
Méthode :
Si
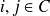 , on dit que
, on dit que
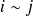 si et seulement si
si et seulement si
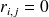 .
.
Fondamental :
Cette relation est :
- réflexive :
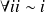
- transitive : évident
-symétrique : Si
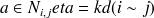 alors
alors
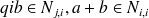 et donc
et donc
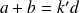 donc
donc
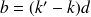 et donc
et donc
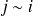 .
.
Définition : Sous classes cycliques
C comporte exactement d classes d'équivalence, appelée les sous -classes cycliques de C.






