Définition
Définition : Le symbole flèche
On introduit une flèche entre i et
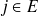si et seulement si
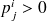
i mène a j, s'écrit donc ainsi :
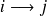
On obtient ainsi un diagramme représentant un graphe orienté.
Fondamental : La relation transitive
On transitive cette relation en disant "i peut conduire à j" si et seulement si il existe un chemin de i vers j.
Ce qui équivaut à :
.
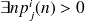i peut conduire à j s'écrit donc :
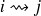
Ce qui signifie qu'il existe un chemin pouvant mener de i à j, en autant de transition que l'on veut. Ce qui diffère de la
relation "i mène à j" , car dans celle ci, le chemin n'est constitué que d'une seule transition.
Fondamental : La relation d'équivalence
On introduit une relation d'équivalence sur E par :
"i et j communiquent si et seulement i=j ou
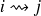et
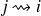
Les états se groupent ainsi en classes d'équivalence, et c'est ainsi que l'on obtient la classification des états.
