| 1 |
|
1 |
|
|
|
|
Le problème posé par le phénomène de fatigue est son aspect aléatoire. En effet, deux roulements identiques, de même marque et fabriqués à partir d’un même lot se détériorent après des durées de fonctionnement très différentes. La durée de vie n’est pas une donnée de précision, mais une notion statistique. La norme ISO 281 donne la durée de vie nominale, dite durée L10 celle qui est atteinte par 90% des roulements essayés dans les mêmes conditions. La fiabilité est donc de 90%, ou la probabilité de défaillance est de 10%.
 | L10 est obtenue en million de tours |  | C : charge dynamique de base ou capacité de charge dynamique (c’est une donnée en Newton : voir dans les catalogues de roulements). C’est la charge pour laquelle un roulement fonctionnant à jeu nul (charge répartie sur la moitié des éléments roulants), a une durée de vie de 1 million de tours. C dépend de la géométrie du roulement, de sa précision d’exécution, de son matériau et de sa marque. |  | P : charge radiale équivalente à calculer en fonction des efforts appliqués par l’extérieur au roulement (en Newton). |  | n = 3 pour les roulements à billes ou les butées à billes. |  | n = 10/3 pour les autres roulements ou butées (à rouleaux, à aiguilles…). |
On peut aussi calculer la durée de vie en nombre d’heures, si on connaît la fréquence de rotation relative N des deux bagues du roulement :
|  Paramètres influant sur la durée de vie : |
|
|
|
| 3 |
3 |
3 |





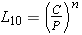


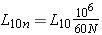


 Paramètres influant sur la durée de vie :
Paramètres influant sur la durée de vie :