Définition

Une charge q, se déplaçant d’un point de potentiel VA à un autre de potentiel VB, dus à des charges extérieures, effectue un travail T= q(VA – VB). On convient que ce travail représente la diminution d’énergie électrostatique du système soit :
Si, de plus, on convient que cette énergie est nulle quand le potentiel l’est en tout point (système totalement déchargé ), alors le travail des forces électrostatiques quand le système passe de l’état actuel à l’état déchargé représente l’énergie électrostatique du système. On peut dire aussi que l’énergie électrostatique du système We = - T , T étant alors le travail des forces au cours de la charge.

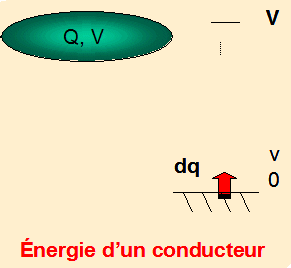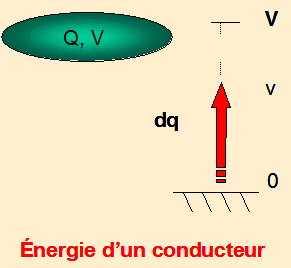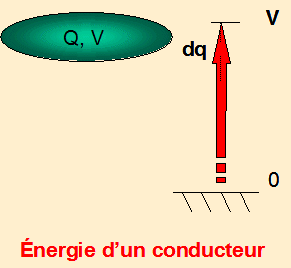
Cas du conducteur unique

Au cours de la charge, par augmentation du potentiel de 0 au potentiel v, compris entre 0 et V final, une charge élémentaire dq passe de 0 à v et le travail correspondant est : dT = dq(0 – v) = - vdq avec dq = C dv , dT = -C v dv. En intégrant de 0 à V , il vient: T = -CV²/2 et l’énergie électrostatique est: