Ampère
a démontré que, dans le vide, mais c’est valable dans
l’air, la circulation de ![]() ,
crée par un courant i, le long d’une trajectoire (c ) qui
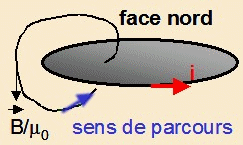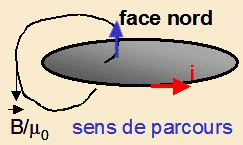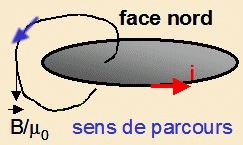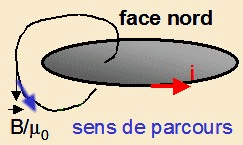
enlace le circuit est : C = i chaque fois que l’enlacement se fait
de la face sud à la face nord du circuit et - i dans le cas contraire.
La face nord est celle de sortie des lignes
de champ donnée par la règle du tire-
bouchon (coté pointe d’un tire- bouchon tournant dans
le sens du courant).
,
crée par un courant i, le long d’une trajectoire (c ) qui
enlace le circuit est : C = i chaque fois que l’enlacement se fait
de la face sud à la face nord du circuit et - i dans le cas contraire.
La face nord est celle de sortie des lignes
de champ donnée par la règle du tire-
bouchon (coté pointe d’un tire- bouchon tournant dans
le sens du courant).
Ce théorème facilite
beaucoup le calcul de B chaque fois que le circuit présente une
symétrie ou que B est uniforme.
Circulation de
Exemple
: calcul de l’ induction créée par un fil rectiligne
indéfini se refermant très loin.
Par symétrie, les lignes d’induction sont des cercles, normaux
au fil, sur lesquels B est constante et auxquels elle est toujours tangente
( faire tourner le bonhomme d’Ampère sur lui-même pour
le voir).
Prenons un cercle pour trajectoire (c ) et décrivons-le dans le
sens
de B il vient: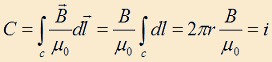
d’où l’on
tire B.
Si on pose ![]() champ
magnétique dans l’air, appelé encore « excitation
magnétique », alors ce théorème dit que
la circulation de
champ
magnétique dans l’air, appelé encore « excitation
magnétique », alors ce théorème dit que
la circulation de ![]() sur
un contour fermé est égal au courant enlacé.
sur
un contour fermé est égal au courant enlacé.
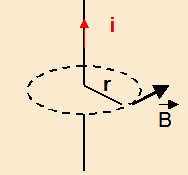
Calcul
de B créé par un fil rectiligne indéfini