Corrigé du problème 3
Rappel : PROBLEME 3
L'objectif est de résoudre une extension du problème précédent avec des durées de latence par un algorithme de programmation dynamique pour les données suivantes. Le critère à minimiser est la date de livraison de la dernière tâche.
paramètre | valeur numérique |
t1 | 11 |
t2 | 14 |
i | 1 | 2 | 3 | 4 |
pi | 4 | 6 | 5 | 2 |
qi | 7 | 4 | 2 | 1 |
Remarque : Dominance de l'ordre de Jackson
On peut remarquer que pour les deux sous-ensembles des tâches ordonnancées avant ou après la période d'indisponibilité, nous devons respecter l'ordre de Jackson (c'est-à-dire, l'ordre correspondant aux durées de latence décroissantes). Cette propriété est connue comme dominante dans le cas d'un problème à une machine sans contrainte d'indisponibilité. C'est pour cette raison que nous avons pris les données de telle sorte que les tâches soient indexées suivant cet ordre.
On peut donc déduire que la solution optimale va consister à affecter chaque tâche avant ou après l'indisponibilité. L'ordre dans chaque partie (avant ou après l'indisponibilité) est celui de Jackson (donc selon l'ordre croissant des indices des tâches).
Méthode : Principe
Le principe de l'algorithme consiste à construire à chaque itération i=0,1,2,...,4 un ensemble Ei contenant des états [t,f] associés à des solutions partielles faisant intervenir les i premières tâches en sachant que :
- t est la durée opératoire totale utilisée avant t1 associée à l'état,
- f est la date de livraison de la dernière tâche dans l'ordonnancement partiel associé à l'état.
Les relations de récurrence, nécessaires pour calculer les états à chaque itération, se basent sur la règle suivante.
Fondamental : Règle d'évolution
Soit [t,f] un état de l'ensemble E(i-1) généré à l'itération i (i=1,2,...,4). A partir de cet état, deux états peuvent être créés dans l'ensemble E(i) à l'itération suivante selon les conditions suivantes :
[t + pi, max{f, t + pi + qi}] si t + pi ≤t1 (ceci implique que la tâche i a été placée avant t1)
[t, max{f, t2+Qi - t + qi}] avec Qi la somme des durées opératoires des i premières tâches (cela implique que la tâche i a été placée après t2).
Méthode : Algorithme (pour n tâches)
E(0)={[0,0]}
Pour i=1,2,3,...,n
Initialiser E(i)={}.
Créer pour chaque [t, f] de E(i-1) deux états [t + pi, max{f, t + pi + qi}] si t + pi ≤t1 et [t, max{f, t2+Qi - t + qi}] et les insérer dans E(i).
Supprimer E(i-1).
Pour chaque valeur t, garder au maximum un état [t, f] dans E(i) avec f minimal.
Retourner min [t, f] dans E(n) {f}
Calcul et résultats
Le détail du calcul est résumé dans le tableau suivant :
i | E(i) |
0 | {[0,0]} |
1 | {[4,11] ; [0,25]} |
2 | {[10,14] ; [4,24] ; [6,25] ; [0, 28]} |
3 | {[10,21] ; [9,24] ; [4,27] ; [11,25] ; [6,25] ; [5,28] ; [0, 31]} |
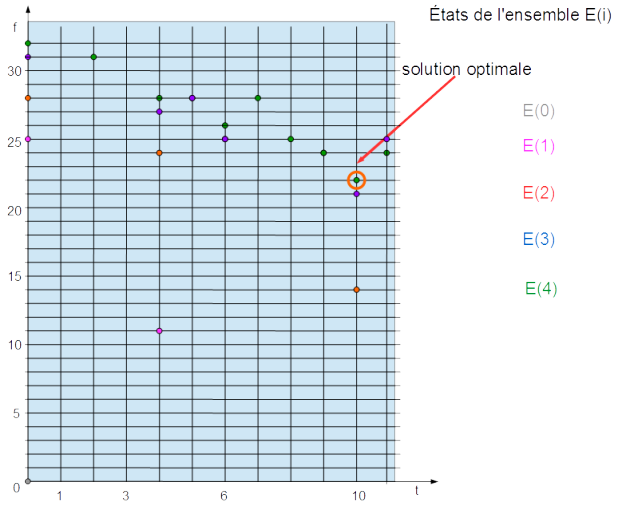
4 | {[10,22] ; [11,24] ; [9,24] ; [4, 28] ; [8,25] ; [6, 26] ; [7, 28] ; [5,28] ; [2,31] ; [0, 32]} |
Le minimum est obtenu pour l'état [10,22] dans E(4), ce qui montre que la date de livraison optimale est égale à 22. Cette solution correspond à affecter les tâches 1 et 2 avant t1 et les tâches 3 et 4 après t2.
L'espace d'états est donné dans la figure suivante (une couleur est associée à chaque ensemble d'états E(i) avec i=0,1,2,3,4).
Fondamental :
Pour n tâches, la complexité de l'algorithme de programmation dynamique est de O(n.t1). En effet, on peut remarquer que le nombre d'états générés à chaque itération est borné par (t1+1). De plus, nous avons (n+1) itérations à réaliser. Ceci conduit également à une complexité calculatoire de O(n.t1).
L'algorithme est donc pseudo-polynomial car t1 peut être exponentiel en fonction de n.
Simulation : Visualiser l'espace d'états
L'ensemble d'états à chaque itération est calculé et représenté dans l'animation suivante. Afin d'assurer une meilleure compréhension de l'algorithme proposé, nous recommandons au lecteur de visualiser le fichier PPS suivant. La grille représente l'espace d'états et les coordonnées des points s'affichant à chaque itération représentent les valeurs des états associés. Il est à noter que la grille est dimensionnée pour que tout état optimal puisse être représenté (t1 pour la variable t et une valeur heuristique (BS=32) pour la variable f). Ici, BS est obtenue à partir de la solution consistant à placer toutes les tâches après t2.
Cette animation facilitera la compréhension de l'exécution étape par étape de l'algorithme.