Illustration de la programmation linéaire en nombres entiers
Exemple : PLNE pour la résolution du problème de sac-à-dos
Afin d'illustrer la méthode de la programmation linéaire à variables entières, nous nous intéressons à un problème particulier où les variables de décision sont binaires (0 ou 1). Nous allons montrer qu'une telle méthode devient dans ce cas une procédure de séparation et d'évaluation particulière grâce à une relaxation réelle de la contrainte d'intégrité.
Reprenons le problème de sac-à-dos classique traité précédemment. On considère une instance de 3 objets définie comme suit :
w₁=10 ; w₂=7 ; w₃=6 ;
v₁=7 ; v₂=4 ; v₃=6 ;
Vmax=10.
Le problème peut donc être représenté sous la forme linéaire suivante :
Maximiser f=10x₁+7x₂+6x₃
tel que :
7x₁+4x₂+6x₃≤10
xi∈{0,1} ∀ 1≤i≤3
Méthode : Les étapes d'exécution de la PLNE
1ère étape : recherche d'une solution heuristique
On peut classer les objets selon le rapport de l'utilité sur le volume wi/vi et ensuite les insérer dans le sac selon ce classement. L'insertion est achevée quand le sac est plein. Dans notre cas, on a : w₁/v₁=10/7 ; w₂/v₂=7/4 et w₃/v₃=6/6. Il s'ensuit que le classement est le suivant : {objet 2, objet 1, objet 3} et que la solution retenue est : x₂=1, x₁=0, x₃=1 ce qui donne une valeur f₁ de la fonction objectif égale à 13.
2ème étape : recherche de la solution optimale
La relaxation de la contrainte d'intégrité binaire (xi∈{0,1}) permet de considérer la résolution du problème à variables réelles et d'appliquer la méthode de résolution linéaire de Simplexe. Sa résolution donne les résultats suivants : x*₁=0, x*₂=2.25, x*₃=0 et f*=15.75.
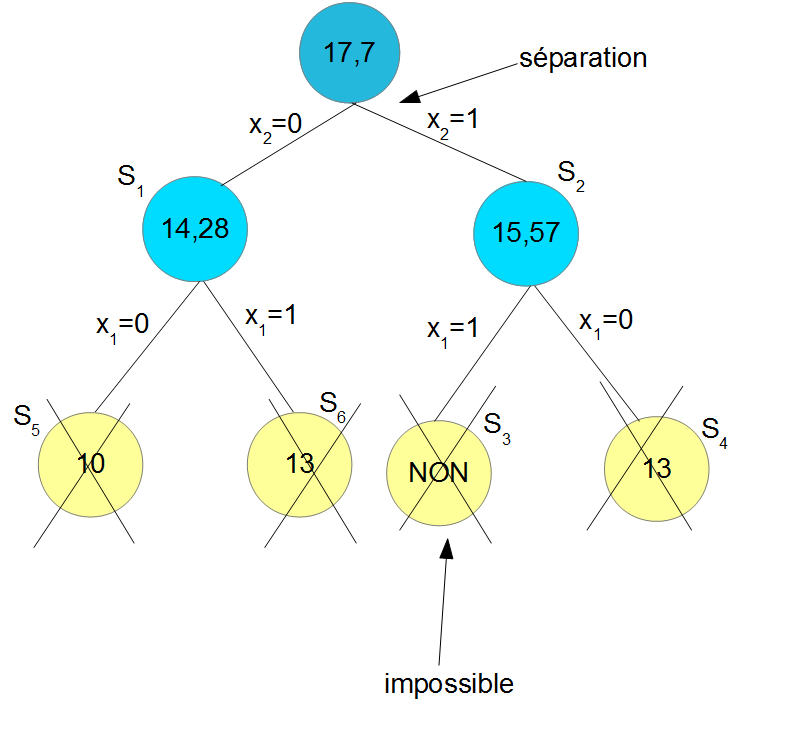
Un tel résultat nous indique que dans le meilleur des cas l'utilité optimale f* ne peut pas dépasser 15.75. On sait également que la solution optimale est meilleure que celle donnée par l'heuristique et que par suite, on peut espérer une valeur de f supérieure ou égale à 13.
La première séparation consiste à considérer les deux cas : x₂=0 et x₂=1 (voir la figure ci-dessus).
Si x₂=0, le système est équivalent à :
Maximiser 10x₁+6x₃
avec
7x₁+6x₃≤10
x₁ et x₃∈{0,1}
Pour ce système d'équations, la relaxation de la contrainte d'intégrité conduit à l'issue de l'application de la méthode de Simplexe à un profit maximal de 14.28 ce qui est supérieur à la valeur f₁ obtenue pour la solution heuristique initiale (voir la branche S₁ dans la figure ci-dessus). Il s'ensuit que l'exploration de cette branche sera suivie.
Pour x₂=1, le système est équivalent à :
Maximiser {10x₁+6x₃}
tel que :
7x₁+6x₃≤6
x₁ et x₃∈{0,1}
La résolution d'un tel système d'équations nous donne un profit maximal de 15.57, la branche sera donc explorée (voir la branche S₂ dans la figure précédente).
Pour la branche S₂, on choisit de séparer avec x₁=1 et x₁=0.
L'hypothèse de x₁=1 est impossible car cela viole la contrainte de volume maximal (nœud S₃ de l'arbre). On sera donc obligé à continuer l'exploration en imposant x₁=0. Pour x₁=0, on calcule la borne supérieure du profit en relâchant la contrainte d'intégrité en imposant x₁=0 et x₂=1 selon les équations :
Maximiser 10×0+7×1+6x₃
tel que :
7×0+4×1+6x₃≤10
x₃∈{0,1}
ce qui donne x₃=1 avec un profit maximal de 13 (nœud S₄ de la figure précédente). Or, la solution heuristique initiale a le même profit et donc c'est inutile d'explorer cette branche.
Pour la branche S₁, la décision x₁=0 nous permet théoriquement d'avoir une borne supérieure de profit égale à 10 (branche S₅ de l'arbre). Il est donc inutile de l'explorer puisque la solution déjà trouvée est meilleure. D'autre part, si x₁=1, les équations deviennent :
Maximiser 10×1+7×0+6x₃
tel que :
7×1+4×0+6x₃≤10
x₃∈{0,1}┊
La résolution d'un tel système d'équations en relâchant la contrainte d'intégrité nous donne une borne supérieure sur le profit égale à 13 unités. Par la suite, il n'est pas opportun d'explorer cette branche (nœud S₆ de l'arbre).
En conclusion, la solution initiale donnée par l'heuristique est optimale. Cela confirme le résultat trouvé en appliquant la méthode de la programmation dynamique.





