Illustration de la programmation dynamique sur un problème de sac-à-dos
Exemple : Instance du problème
Pour illustrer cette méthode, nous allons considérer un problème d'optimisation combinatoire très connu. Il s'agit du problème du "sac à dos". Imaginons que vous partez en vacances et que vous êtes en train de préparer votre sac à dos. Vous avez un ensemble de n objets à prendre mais malheureusement, le volume de votre sac est limité. Chaque objet i est caractérisé par un volume vi et par une importance ou une utilité wi (∀ 1≤i≤N). Le problème est donc de choisir une partie de ces objets de telle manière que l'on ne dépasse pas le volume maximal Vmax tout en maximisant la somme des profits associés aux objets sélectionnés. On peut donc associer à chaque objet i, une variable de décision binaire xi qui vaut 1 si l'objet est sélectionné et qui vaut 0 sinon. Ainsi, le problème est formulé comme suit :
Maximiser ![]()
tel que :
![]()
![]()
Considérons maintenant l'instance du problème avec les paramètres suivants :
![]()
Il s'ensuit que notre problème P peut être formulé comme suit :
Maximiser 11x₁+8x₂+5x₃
tel que :
7x₁+6x₂+4x₃≤10
![]()
Formulation du prolongement et définition de la récurrence
Le problème P peut donc être prolongé en un problème P(n,V) défini de la manière suivante :
Maximiser ![]()
tel que :
![]()
![]()
avec n et v deux entiers naturels et Fn,v est le maximum de la valeur de la fonction objectif pour le problème P(n,v).
La résolution de P se ramène à résoudre P(3,10). Pour ce faire, la programmation dynamique consiste à résoudre les problèmes P(n,v) de proche en proche en utilisant la relation de récurrence suivante :
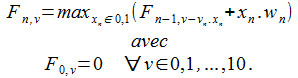
En effet, le maximum de la fonction objectif, associé à la décision xn, est la somme de l'utilité apportée par cette décision (wn.xn) et de l'utilité maximale des (n-1) autres objets pour le volume laissé après la prise de la décision xn (c'est à dire v-xn.vn). Ce principe est illustré dans la figure suivante.
L'application de la méthode de la programmation dynamique donne le tableau suivant indiquant la valeur de l'utilité maximale Fn,v.
Calcul et résultats
Le détail du calcul est résumé dans le tableau suivant :
n \ v | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 | 11 | 11 | 11 |
2 | 0 | 0 | 0 | 0 | 0 | 0 | 8 | 11 | 11 | 11 | 11 |
3 | 0 | 0 | 0 | 0 | 5 | 5 | 8 | 11 | 11 | 11 | 13 |
La valeur maximale est obtenue pour F3,10 et est égale à 13.
F3, 10=F2, 10-1×4+(x₃=1)×5 ce qui correspond à prendre x₃=1 ;
F2, 10-1×4=F2, 6=8=F1, 6-(x2=1)×6+8×(x2=1) ce qui correspond à prendre x₂=1 ;
F1, 6-1×6=F1, 0=0 ce qui correspond à ne pas prendre le premier objet. En conclusion, la solution optimale est la suivante :
x₁=0, x₂=x₃=1 avec F3, 10=5+8=13.
Fondamental :
D'une manière générale, la rapidité de la méthode est directement liée au nombre d'états calculés. Ici, la complexité de l'algorithme de programmation dynamique est de O(N.Vmax). En effet, on peut remarquer que le nombre d'états générés correspond au nombre de cases du tableau (c'est-à-dire, (N+1)(Vmax+1)), ce qui conduit à une complexité de O(N.Vmax). Cette complexité est dite pseudo-polynomiale (la donnée Vmax peut être exponentielle en fonction de N).






