Illustration sur un problème d'ordonnancement à une machine
Dans cette section, nous présentons une illustration de la méthode sur un problème d'ordonnancement sur une machine. Pour un rappel sur les problèmes d'ordonnancement, le lecteur est invité à consulter le chapitre sur les graphes [Projet ENSROTICE, Portmann, 2013].
Exemple : Instance du problème
Afin d'illustrer cette méthode, nous proposons son application au problème d'ordonnancement à une machine. Ce problème consiste à ordonnancer un ensemble U de cinq tâches : U={A,B,C,D,E}. Chaque tâche peut commencer après une date ri (date de début au plus tôt) et doit durer pi unités de temps (1≤i≤5). Nous cherchons à construire un ordonnancement réalisable en minimisant le makespan (date de fin d'exécution de la dernière tâche). Le problème se ramène donc à trouver la séquence optimale des tâches sur la machine. Les données du problème sont présentées dans le tableau suivant. La préemption des tâches est interdite et la machine est disponible à tdisp =0.
tâche | A | B | C | D | E |
ri | 0 | 4 | 8 | 7 | 11 |
pi | 4 | 2 | 1 | 3 | 4 |
Remarque :
Le problème en question est un problème polynomial. La solution optimale peut être simplement obtenue en ordonnançant les tâches dans l'ordre croissant des ri (règle FIFO ou First In First Out). L'objectif de cet exemple est tout simplement d'illustrer la procédure de séparation et d'évaluation et de montrer qu'elle trouve bien la solution optimale pour ce problème particulier. Dans la suite, nous donnons le détail de la résolution de l'exemple.
Pour commencer : une solution heuristique
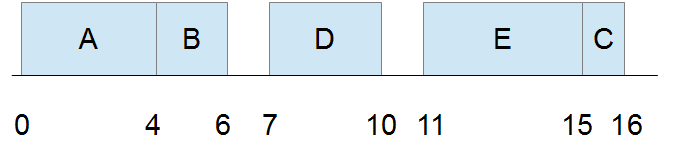
La solution heuristique que nous choisissons est la suivante : ABDEC. Elle est représentée dans le diagramme de Gantt de la figure suivante. Cette solution est caractérisée par une valeur de la fonction objectif égale à b₀=16.
Borne inférieure
La borne inférieure proposée ici se base sur la relaxation de la contrainte de disponibilité des tâches. Il est donc clair que pour exécuter un sous ensemble V ⊂U , le temps nécessaire est minoré par la valeur B(V) définie comme suit :
Cette borne va nous servir à évaluer la performance de chaque branche séparée.
L'étape initiale consiste à évaluer la borne inférieure pour l'ensemble U (car on n'a pas encore séparé l'ensemble des solutions possibles). On trouve B(U)=14, ce qui correspond à l'évaluation de la branche primaire (voir l'arborescence à la fin de cet exemple). Par la suite, la solution optimale de notre problème a une valeur de critère comprise entre 14 et 16.
Schéma de séparation et d'exploration
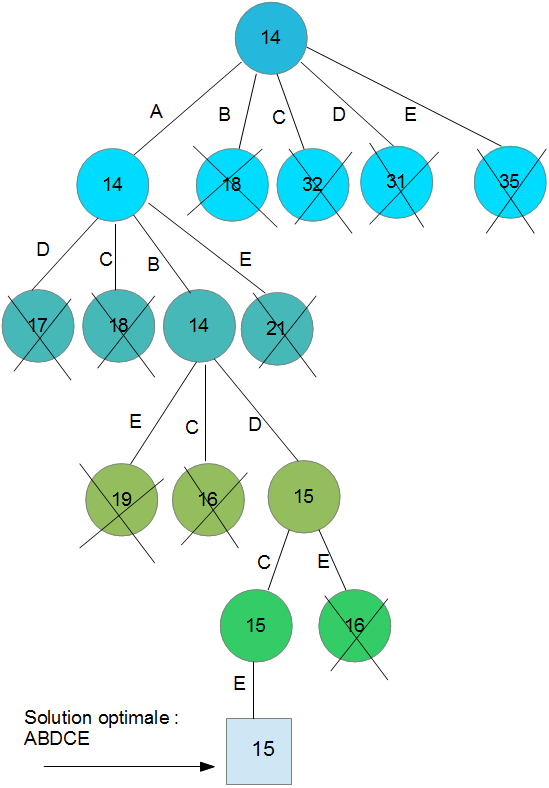
La règle de séparation choisie consiste à considérer plusieurs niveaux dont le nombre est égal à celui de tâches à réaliser. A chaque niveau on décide de séquencer une tâche sur la machine parmi toutes les possibilités qui sont envisageables. Ainsi, on commence au début de la procédure par séparer selon la tâche qui s'exécute à la première position. Évidemment, cinq cas sont possibles : A, B, C, D ou E. Cela génère donc cinq branches que nous devons évaluer (voir l'arborescence ci-dessous). Dans cette arborescence la valeur indiquée dans chaque nœud correspond à la valeur de la borne inférieure (et à la valeur de la fonction objectif dans un nœud terminal).
Considérons par exemple la branche correspondant à commencer l'ordonnancement par la tâche A. Dans ce cas, A sera réalisée durant l'intervalle [0, 4]. Par la suite, la machine sera disponible à tdisp=4 et l'ensemble des tâches restant à réaliser est V={B,C,D,E}. Il s'ensuit que l'évaluation de cette branche, en appliquant la formule de la borne inférieure, donne le résultat suivant : B(V)=max{4,min{4,8,7,11}}+2+1+3+4=14, ce qui impose l'exploration de cette branche car 14<b0 (voir l'arborescence).
L'application du même raisonnement sur la branche correspondant à commencer l'ordonnancement par la tâche B conduit à une évaluation de 18>b0 (voir l'arborescence). Il est donc inutile d'explorer cette branche puisque l'on dispose déjà d'une solution dont la valeur du critère est meilleure. Cela permet donc d'écarter plusieurs possibilités moins bonnes que la solution courante et diminuer la taile de l'arborescence. L'exploration est donc bien implicite. L'évaluation des autres branches conduit également à conclure l'inutilité de leur exploration. Un résultat pertinent est donc conclu à l'issue de l'exploration de ce premier niveau : pour aboutir à une solution optimale, il faut obligatoirement commencer l'ordonnancement par exécuter la tâche A.
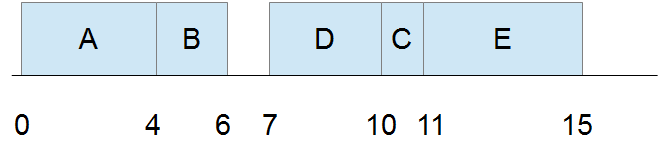
La méthode est poursuivie en employant la même démarche. L'application de la méthode de proche en proche conduit à l'arborescence représentée dans la figure ci-dessus. L'ordonnancement optimal correspond donc à la séquence ABDCE (qui correspond bien à la séquence FIFO). Il est représenté dans la figure suivante.
Fondamental :
D'une manière générale, la rapidité de la méthode, liée directement au nombre de branches visitées, dépend de la qualité de borne inférieure et de celle de la borne supérieure. De plus, le schéma de séparation (branchement) utilisé a une influence importante sur le temps de calcul. On peut également choisir différentes stratégies d'exploration en largeur, en profondeur ou toute combinaison des deux. Tous ces ingrédients forment un ensemble de leviers permettant de concevoir de nombreuses variantes de cette méthode pour un même problème. Les meilleurs réglages sont généralement spécifiques à chaque problème.