Structure générale des méthodes d'amélioration par voisinage
Dans cette partie, nous allons tout d'abord définir la notion de voisin, puis nous présentons les différents schémas d'algorithmes d'amélioration par voisinage en commençant par les heuristiques simples et en terminant par les méta-heuristiques.
Comme pour les algorithmes génétiques, nous nous intéressons à la résolution de problèmes d'optimisation et nous souhaitons explorer l'ensemble des solutions de manière à en extraire une solution aussi bonne que possible sans garantie que la meilleure solution trouvée soit optimale.
Définition : Voisin
Voisin est un opérateur unaire qui à une solution S fait correspondre une solution v(S), en appliquant une modification (généralement locale) à la solution S.
Une solution S peut avoir plusieurs voisins.
V(S) est l'ensemble des voisins de S.
v(S) est un des voisins de S (choisi, par exemple, de manière aléatoire).
Présentation intuitive et algorithmique des méthodes de voisinage
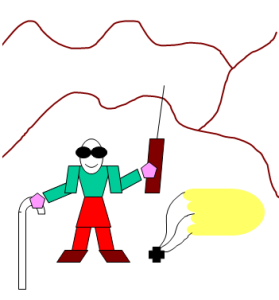
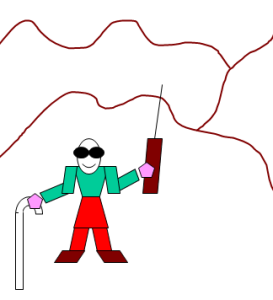
Pour présenter les méthodes par voisinage, nous allons illustrer l'approche en nous appuyant sur la démarche d'un aveugle ou d'un mal voyant qui doit rechercher le point le plus bas d'une montagne.
Espace des évaluations de l'espace des solutions
 | La montagne ci-contre représente les variations du niveau de la fonction à minimiser en supposant que l'on peut étaler les solutions du problème sur une surface et représenter les valeurs de la fonction à minimiser par une altitude en chaque point de la surface. L'objectif est de trouver le fond de la vallée. |
Exploration locale de l'espace des solutions : solution initiale
 | Un aveugle est parachuté en un point de départ quelconque xo sur la surface. L'aveugle est muni d'un appareil lui permettant de mesurer son altitude (valeur de la fonction objective à minimiser au point où il se trouve), son positionnement (paramètres décrivant la solution associée au point où il se trouve) et capable en outre de transmettre ces mesures à un système central. Il est également muni d'une canne qui lui permet de tâter autour de lui de manière à explorer le voisinage du point où il se trouve. Son voisinage est d'autant plus important que sa canne est grande. Il est capable d'examiner toutes les solutions de son voisinage qui sont à portée de sa canne et de connaître leur altitude. |
Première méthode : méthode de plus forte pente
 | L'aveugle cherche le point le plus bas de son voisinage et s'y rend s'il est strictement plus bas que le point où il se trouve. Sinon, il reste où il est et conclut qu'il a atteint le point le plus bas du paysage. |
Description de la méthode de plus forte pente
Initialisation
xo est une solution choisie de manière aléatoire ou obtenue en utilisant une heuristique simple construisant une solution.
f(xo) est la valeur de la fonction objective à minimiser au point xo.
FIN = faux ;
Itérations
tantque FIN == faux faire
FIN = vrai ;
meilleur = xo ;
mini = f(meilleur) ;
pour tout x de V(xo) faire
nouveau = f(x);
si (f(x)<mini) alors
FIN = FAUX ;
meilleur = x ;
mini = f(meilleur);
finsi ;
fin pour tout x ;
xo = meilleur;
fin tant que
xo et meilleur contiennent la meilleure solution trouvée
| La méthode s'arrête dans un optimum local lorsque aucun point du voisinage n'est strictement meilleur que le point où se trouve l'aveugle. Si l'aveugle tombe sur un glacier, juste à côté d'une profonde crevasse. Il va rapidement croire qu'il a atteint le bas de la montagne et s'arrêter. |
Attention :
S'il y a une zone plane autour de l'aveugle, on pourrait penser qu'il pourrait encore progresser si on acceptait qu'il se déplace pour une altitude égale à celle où il se trouve.
Mais dans ce cas, l'algorithme pourrait se mettre à boucler sur un sous-ensemble de solutions voisines qui ont toute la même valeur.
On verra plus loin une méthode qui cherche à éviter type de problème.
Amélioration de toute méthode qui se termine sur un minimum local
 | On applique la même méthode avec plusieurs points de départ aléatoires. Ce qui, dans notre présentation intuitive, revient à parachuter un escadron d'aveugles dans des points les plus éloignés possibles les uns des autres sur la montagne. |
Remarque :
Si le voisinage est grand, cela peut prendre beaucoup de temps pour examiner le voisinage complet d'un point, sauf si on dispose d'une technique pour trouver rapidement le meilleur point du voisinage (sans obligatoirement tout explorer).
C'est pour cette raison que beaucoup de méthodes par voisinage se contente du premier point visité meilleur que le point où on se trouve.
Seconde méthode : Méthode de descente ou "hill climbing"
 | L'aveugle choisit le premier point qu'il examine lui permettant de diminuer strictement son altitude. |
Remarque :
Ou bien l'aveugle examine toujours son voisinage de manière systématique et sait quand il a fini d'explorer son voisinage sans avoir obtenu une amélioration.
Ou bien l'aveugle choisit un voisin de manière totalement aléatoire.
En cas de choix aléatoire, on est néanmoins obligé de faire une exploration systématique du voisinage, si, par exemple, après N essais on n'a pas changé de position. Si on ne faisait pas ce test, l'algorithme pourrait boucler sur chercher un voisin du point où on se trouve de manière aléatoire pour essayer d'en trouver un meilleur.
Dans tous les cas, on arrête l'algorithme de la même façon que dans le cas de la méthode de descente.
Description de la méthode de descente
Initialisation
xo est une solution choisie de manière aléatoire ou obtenue en utilisant une heuristique simple construisant une solution.
f(xo) est la valeur de la fonction objective à minimiser au point xo.
FIN = faux ;
J = 0;
Itérations
tantque FIN == faux faire
FIN = vrai ;
x = v(xo) ;
si(f(x)<f(xo) alors
FIN = FAUX;
J = 0 ;
xo = x ;
sinon
J = J+1;
si J > N alors
vérification pour voir si on est dans un optimum local
meilleur = xo ;
mini = f(meilleur) ;
pour tout x de V(xo) (tant que FIN == VRAI) faire
nouveau = f(x);
si (f(x)<mini) alors
FIN = FAUX ;
meilleur = x ;
mini = f(meilleur);
finsi ;
fin pour tout x ;
xo = meilleur;
fin si ; fin de la vérification pour voir si on est dans un optimum local
fin si ; fin du cas initialement non améliorant
fin tant que fin de la progression d'un pas de l'aveugle
xo et meilleur contiennent la meilleure solution trouvée
Troisième méthode : marche stochastique
Cette méthode n'est en général pas enseignée, nous la présentons ici car c'est en fait une méthode intermédiaire entre la méthode précédente et la méthode du recuit simulé que nous verrons ensuite.
Nous ne décrivons pas l'algorithme correspondant.
| L'aveugle erre de manière totalement aléatoire, on retient la meilleure position visitée. Arrêt par fatigue (après avoir visité N points). |
Inconvénient : si la surface a des régularités avec des pentes vers les positions les plus basses, on ne profite absolument pas de la configuration du paysage.
Avantage : on n'est jamais piégé dans un optimum local.
Quatrième méthode : Marche stochastique hybridée de plus forte pente.
Cette méthode n'est en général pas enseignée, nous la présentons ici car elle a été expérimentée avec un certain succès un problème d'optimisation.
Nous ne décrivons pas l'algorithme correspondant.
| En alternance, on choisit un voisin aléatoire et en alternance on retient la meilleure solution visitée Arrêt par fatigue (après avoir visité N points). |
Elle corrige partiellement l'inconvénient de la méthode précédente.
Avantage : on n'est jamais piégé dans un optimum local.
Cinquième méthode : le recuit simulé
| Au départ l'aveugle est plein d'énergie et il accepte aléatoirement de remonter si la remontée n'est pas trop forte et si son énergie est suffisante. L'aveugle perd progressivement son énergie et on termine par une méthode de descente lorsqu'il n'a plus d'énergie. |
Cette méthode est issue de la thermodynamique en recherchant à reproduire un recuit simulé dans un algorithme.
Inspiration à partir de la thermodynamique
Pour que la structuration finale d'un corps soit harmonieuse, il est nécessaire qu'il passe par des phases intermédiaires moins favorables pour atteindre son état final, état qu'il ne pourrait peut-être jamais atteindre si on cherchait une suite d'états qui tendent de manière uniforme et régulière vers l'état souhaité.
A haute température, le corps passe par de nombreux stades de transformation qu'il atteint facilement grâce à l'énergie liée à la température,
plus la température baisse et plus les transformations sont régulières et orientées vers l'état final.
Notations utilisées dans l'algorithme
une température T qui décroît par paliers de longueur N de manière exponentielle, par l'utilisation du paramètre a (0<a<1).
un générateur aléatoire de voisins VOISIN(x) qui fournit au hasard une solution (admissible) dans le voisinage de la solution (admissible) x.
une fonction objective f(x) que l'on cherche par exemple à minimiser.
la meilleure solution trouvée depuis le début xm et sa valeur fm.
un nombre maximal d'itérations sans amélioration Q
on répète P fois l'algorithme avec un nouveau point de départ aléatoire.
Schéma général du refroidissement
pour k de 1 à P faire
un essai
Initialisation de l'essai
xo:=solution aléatoire; Solution de départ
fm:=f(xo); Initilisation meilleure valeur
J:=0; Initialisation compteur arrêt
T:=To; Initialisation Température
Déroulement de l'essai
tantque J ≤ Q faire
Palier température
I:=0; Initialisation compteur palier
Boucle sur les essais élémentaires au sein du palier
........................
........................
(les détails sont dans le listing suivant)
Fin palier température
T:=T*a;
fintantque
retenir fm , xm;
finpour (k) Fin essai
Le résultat est lameilleure solution trouvée par l'ensemble des essais.
Boucle interne à température constante
tantque I ≤ N et J ≤ Q faire
x1:=VOISIN(xo); une tentative de progression
I:=I+1; incrémentation du compteur pour le palier de température
J:=J+1; incrémentation du compteur pour l'arrêt final d'un essai
si f(x1) < f(xo) alors
xo:=x1;
si f(xo)<fm alors
xm:=xo;
fm:=fo;
J:=0;
finsi;
sinon
∆f:=f(x1)-f(xo);
U:=Uniforme(0,1);
si U ≤ exp (- ∆f / T) alors
xo:=x1
finsi
finsi;
fintantque
Remarque :
Si le point x1 est strictement meilleur que le point xo. Il remplace xo et si la solution est meilleure que la meilleure solution trouvée dans l'essai, on corrige la meilleure solution trouvée et on remet à 0 le compteur de fin.
Si le point x1 n'est pas strictement meilleur que le point xo. Il remplace xo avec la probabilité exp(-perte/température).
La probabilité d'accepter de passer à un point plus mauvais est donc d'autant plus grande que la perte est faible et que la température est grande.
Sixième méthode : La méthode Taboue et ses variantes
Comme le recuit simulé, la méthode Taboue permet d'accepter des solutions plus mauvaises de manière à éviter de se faire piéger dans un optimum local.
La méthode Taboue utilise la mémoire de manière à éviter de repasser plusieurs fois par les points visités.
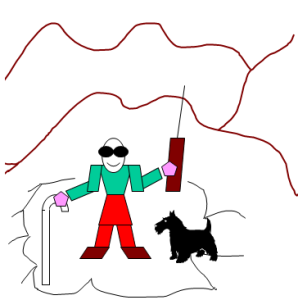
 | On accepte de remonter pour pouvoir quitter les optima locaux, mais pour ne pas y retomber, on place des « tabous » qui empêchent de retourner aux points déjà visités. Sur notre présentation intuitive, nous avons ajouté un petit chien qui peut renifler et refuser que l'aveugle repasse là où il est déjà passé. |
Avantage : la méthode ne peut pas boucler.
Inconvénient : si on garde la description de toutes les solutions déjà visitées, le besoin en mémoire peut être très grand et en outre, on passe de plus en plus de temps à tester si la nouvelle solution a déjà été visitée en la comparant à toutes celles qui sont en mémoire.
Phénomène de blocage de la méthode Taboue
 | Si lorsque l'on atteint un point, on a visité auparavant tous ses voisins, alors la méthode s'arrête sur ce point puisqu'on ne trouve plus de voisins non visités du point courant. |
Première variante de la méthode Taboue
Pour éviter d'encombrer inutilement la mémoire et de perdre trop de temps à comparer un point avec tous les points déjà visités, on limite à L le nombre de points visités que l'on conserve en mémoire et on appelle cette liste de L points la liste Taboue L.
Remarque :
Le fait de limiter à L la taille de la liste Taboue ne fait pas totalement disparaître les problèmes de blocage, sauf si L est vraiment très petit.
Phénomène de bouclage
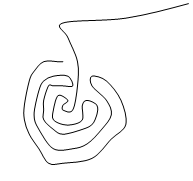 | Si L est trop petit, le fait que les points les plus anciennement visités disparaissent fait que l'on peut retomber sans cesse dans le même optimum local. |
Deuxième variante de la méthode Taboue
Souvent, la méthode VOISIN possède un inverse.
Par exemple, pour le codage binaire : si on a inversé la valeur du gène i, alors on revient au point précédent en inversant à nouveau le gène I.
De même, pour le codage de permutation : si on a échangé la valeur des gènes i et j, alors on revient au point précédent en échangeant à nouveau la valeur des gènes i et j.
Une variante de la méthode Taboue consiste à mettre dans la liste Taboue, non pas des solutions, mais la liste des mouvements inverses qui permettraient de revenir aux solutions précédentes (en les suivant dans l'ordre).
C'est une variante très utilisée.
En général, cette méthode ne conduit à aucun blocage, par contre, on peut boucler.
