Structure générale des algorithmes génétiques
Présentation historique
Les algorithmes génétiques (AG ou GA dans la littérature en anglais) sont des méthodes approchées car ils ne s'appuient pas, dans leur conception, sur des théorèmes qui permettent d'affirmer que la meilleure solution obtenue en un temps fini est optimale.
Ils ont été créés par analogie avec des phénomènes naturels.
Ils simulent l'évolution naturelle d'organismes (individus), génération après génération, en respectant des phénomènes d'hérédité lors de reproduction par croisement ou mutation et une loi de survie.
Dans une population d'individus, ce sont en général les plus forts, c'est-à-dire les mieux adaptés au milieu, qui survivent et donnent une descendance.
Par ailleurs, on suppose que les qualités et les défauts peuvent être hérités des parents de manière stochastique ou déterministe.
De tels algorithmes furent développés dès 1950 par les biologistes, ensuite ces algorithmes ont été adaptés pour la recherche de solutions de problèmes d'optimisation, en développant une analogie entre un individu dans une population et une solution d'un problème dans un ensemble de solutions.
Remarque : Hypothèses d'évolution des populations
Dans la version standard des algorithmes génétiques, on suppose en général que
Les bons chromosomes doivent avoir une probabilité plus grande d'être choisis comme parents.
Le mariage de bons parents devraient donner de bons enfants.
Les bons chromosomes doivent avoir une meilleure chance de survivre.
Les croisements cherchent à conserver les meilleures caractéristiques des parents.
Le rôle des opérateurs de mutation est de créer de la diversité de manière à éviter la dégénérescence.
Mais certains schémas d'algorithmes génétiques peuvent utiliser des hypothèses différentes.
Remarque : Diversité des techniques d'évolution des populations
Comme la nature et les phénomènes d'évolution des populations sont très riches, selon les modèles naturels qui ont inspiré les développeurs d'algorithmes génétiques, plusieurs schémas de reproduction ont été conçus.
Néanmoins, on peut les classer en deux grandes familles.
1) Le modèle associé, par exemple, à la reproduction des papillons, où les parents sont tous morts à la fin de l'été précédent et où la nouvelle population est constituée des enfants de la population précédente. C'est un modèle où population et génération sont confondues.
2) Le modèle associé, par exemple, à la reproduction des mammifères, où la durée de vie des individus est suffisamment longue pour que les arrières petits enfants puissent connaître leurs arrières grands parents et où les accouplements peuvent se produire entre générations différentes. Dans ce modèle, ce sont des populations qui sont modifiées à chaque itération des algorithmes et la notion de génération n'a plus de sens.
Définition : Individus ou chromosomes ou génotypes
Les éléments d'une population sont appelés des individus ou des chromosomes ou des génotypes
Illustration d'une population et de ses individus
On s'est placé ici dans le cas des problèmes d'optimisation à résoudre où on doit explorer l'espace des solutions de manière à essayer de trouver la meilleure solution possible.
Définition : Gènes et allèles
Les différents éléments d'un chromosome ou génotype sont appelés des gènes.
Les différentes valeurs que peuvent prendre les gènes sont appelés les allèles.
Définition : Évaluation d'un chromosome
On appelle force ou fitness une valeur calculée associée à chaque chromosome.
Les schémas généraux des algorithmes génétiques supposent qu'un chromosome est d'autant meilleur que sa force est grande.
Définition : Opérateur génétique de croisement
Un opérateur génétique de croisement est un opérateur binaire (éventuellement p-aire)
qui, en utilisant les gènes de deux (ou de p) chromosomes appelés père et mère ou encore parent 1, parent 2, ..., parent p,
conçoit, un ou plusieurs nouveaux chromosomes, appelés les enfants, parfois sexués (fils ou fille).
Illustration des opérateurs de croisement agissant sur une population
L'opérateur de croisement utilisé ici est binaire.
Il est à noter qu'un même individu peut être parent plusieurs fois en s'accouplant avec des individus différents.
Qualité attendue des croisements
Dans la reproduction naturelle, les individus sont supposés être capables de s'adapter pour mieux résister à leur environnement.
Pour cela, la majorité des enfants doit pouvoir récupérer les bonnes caractéristiques génétiques de leurs parents.
Lorsque les individus sont des solutions de problèmes, le croisement doit fournir des solutions, de préférence réalisable et si possible de bonne qualité.
Si les croisements sont capables de conserver les bonnes caractéristiques des parents et de fabriquer des solutions de bonne qualité, on dit qu'ils jouent le rôle d'opérateur d'intensification.
Dans les méta-heuristiques, les opérateurs d'intensification ont pour objectif d'essayer d'obtenir les meilleures solutions possibles dans l'environnement de solutions déjà connues.
Si les croisements sont totalement aléatoires, il joue le rôle d'opérateur de diversification.
Dans les méta-heuristiques, les opérateurs de diversification ont pour objectif d'essayer de concevoir de nouvelles solutions très différentes des solutions déjà connues.
Définition : Opérateur génétique de mutation
Un opérateur génétique de mutation est un opérateur unaire
qui, en utilisant les gènes d'un chromosome,
conçoit un nouveau chromosome, appelé mutant.
Illustration des opérateurs de mutation agissant sur une population
Qualité attendue des mutants
Dans la reproduction naturelle, les mutants sont sensés éviter les dégénérescences, car certains allèles qui ont une probabilité plus faible d'être conservés lors de la reproduction peuvent disparaître ce qui amène la création d'individu dégénéré qui ne peuvent plus posséder certaines qualités.
Lorsque les individus sont des solutions de problèmes, les mutations sont donc essentiellement des opérateurs de diversification.
Opérateur génétique de mutation améliorante
Lorsque les individus sont des solutions de problèmes, on peut utiliser des opérateurs unaires d'intensification. Ils sont conçus de la même façon que les opérateurs de voisinages correspondant aux méta-heuristiques d'amélioration par voisinage.
Dans ce cas, on modifie les gènes d'un individu avec pour objectif de l'améliorer.
Si on utilise de tels opérateurs dans un algorithme génétique, il s'appelle alors un algorithme mémétique.
C'est une manière de croiser les avantages de différentes types de méta-heuristiques.
Schémas généraux des algorithmes génétiques
Nous allons maintenant intégrer les opérateurs génétiques dans différents schémas d'algorithmes génétiques.
Les deux schémas proposés ont été publiés par leurs auteurs en 1989.
Schéma simple de Goldberg
a- INITIALISATION :
Générer une population initiale Po de N individus.
b- ÉVALUATION :
Évaluer la "force" de tout individu de la population Pn-1.
c- SÉLECTION :
Sélectionner N/2 couples d'individus dans la population Pn-1.
d- CROISEMENT :
tout couple d'individus est
- avec la probabilité pc remplacé par un nouveau couple d'individus
obtenu en lui appliquant un opérateur génétique de croisement,
- avec la probabilité 1-pc conservé.
e- MUTATION :
tout individu
- avec la probabilité pm subit une mutation,
- avec la probabilité 1-pm est conservé.
f- ARRÊT :
on reprend en b- jusqu'à avoir effectué un nombre donné d'itérations (variantes possible : autre condition d'arrêt, voir plus loin).
g- RESULTAT :
Un des chromosomes qui a la meilleure force.
Le schéma simple de Goldberg s'inspire de la reproduction des papillons (sans recouvrement entre les populations successives). |
Schéma de Davis
1) Créer une population initiale de N chromosomes.
2) Evaluer chaque chromosome de la population.
3) Créer Q nouveaux chromosomes par croisements ou par mutations.
4) Détruire certains anciens chromosomes pour faire de la place pour les nouveaux.
5) Evaluer les nouveaux chromosomes et les insérer dans la population.
6) Si la condition d'arrêt est vérifiée
alors
arrêt et retour de la meilleure solution créée
sinon aller à 3)
finsi
Condition d'arrêt =
- un nombre maximal de générations
ou
- une durée maximale pour l'exécution
ou
Un nombre maximal de générations sans amélioration stricte de la meilleure solution trouvée.
 | Le schéma de Davis s'inspire de la reproduction des mammifères (avec recouvrement entre les populations successives). |
Paramètres des schémas
Les deux schémas comportent des paramètres :
N : la taille de la population,
pc : la probabilité de croisement,
pm : la probabilité de mutation,
MAX : le nombre maximal de générations ou la durée maximale attribuée à l'algorithme ou le nombre maximal de générations sans améliorer la meilleure solution trouvée
Q : le nombre de nouveaux chromosomes créés par croisement ou mutation.
D'autres paramètres devront être définis pour la sélection et pour les adaptations spécifiques à un problème donné.
Remarque :
Il n'y a pas de valeurs idéales pour les paramètres associés aux algorithmes génétiques.
Les utilisateurs d'algorithme génétique font des expériences et retiennent de manière expérimentale les paramètres qui semblent les meilleures pour un problème donné et pour la taille des instances des problèmes concrets à résoudre.
Sélection des individus
Quelque soit le schéma général des algorithmes génétiques, il nécessite de sélectionner les individus qui vont être croisés afin de se reproduire.
Les algorithmes génétiques différent selon la manière de calculer et d'utiliser la force pour effectuer des sélections.
Lorsque les individus sont des solutions de problèmes, la meilleure solution S* est celle qui optimise un critère donné ou une fonction objectif donnée g(S*).
Si l'optimum correspond à un minimum, la valeur du critère ne peut pas être utilisée comme force ou fitness du chromosome, il faut la remplacer, par exemple par MAX-g(S).
Souvent, on n'utilise pas g(S) ou MAX-g(S) à maximiser comme valeur pour la fitness, car si g(S) ou MAX-g(S) est grand pour tous les chromosomes, alors ils peuvent avoir presque tous à peu près le même ordre de grandeur et on a du mal à les différencier dans les techniques de sélection.
Exemple de calcul de fitness à partir de la valeur du critère g(S)
1) Constituer la liste S1, S2, S3, .... de chromosomes triés par valeur croissente de g(S).
2) Attribuer à chaque chromosome une fitness égale à son rang :
f(S1) = 1; f(S2) = 2; f(S3) = 3; ...
Attention : Technique de pénalisation et force des individus
Lorsqu'il est difficile de construire des solutions réalisables pour un problème, au lieu d'explorer l'espace des solutions réalisables (qui vérifient toutes les contraintes), on explore un espace plus facile à visiter, mais plus grand, où certaines familles de contraintes (voire toutes les familles de contraintes) ne sont pas vérifiées.
Dans ce cas, il faut être capable de reconnaître les solutions qui ne sont pas réalisables et essayer de mesurer dans quelle mesure elles sont éloignées des conditions de faisabilité.
Pour cela on peut compter le nombre de contraintes non vérifiées ou encore calculer une distance entre la solution non réalisable et l'espace des solutions réalisables. On obtient ainsi une pénalisation p(S).
La valeur que l'on va alors utiliser pour calculer la force d'une solution ne sera plus seulement la fonction objectif g(S), mais la fonction objectif pénalisée : g(S)-p(S).
Bien sûr, on va retenir en fin d'algorithme génétique la meilleure solution trouvée parmi les solutions réalisables.
Exemple de sélection à partir de la force : la technique de la roulette
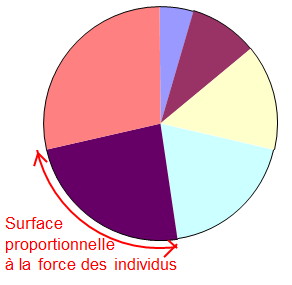 | On attribue à chaque individu d'une population une probabilité d'être reproduit qui est proportionnelle à sa force. Si la force est une valeur entière, cela revient à avoir sur une roulette un nombre de cases qui correspond à la force. |
Exemple d'amélioration de la sélection : la technique du tournoi
Lorsque l'on souhaite que les parents sélectionnés soient de très bonne qualité, on sélectionne, par exemple, avec la technique de la roulette, un sous-ensemble de Q parents candidats à la reproduction, mais on ne retient que les Q' meilleurs du sous-ensemble comme parents effectifs pour la reproduction.
Il faut néanmoins faire attention à conserver un minimum de diversités des parents utilisés pour éviter une dégénérescence que les mutations ne pourraient plus empêcher car les mutants de qualité moindre ne pourraient pas se reproduire.
Conclusion
Nous venons de donner tous les ingrédients qui permettent de construire des algorithmes génétiques, à condition de savoir enregistrer des solutions d'un problème donné sous forme de gènes dans des chromosomes, de savoir évaluer les chromosomes pour obtenir g(S) (et éventuellement p(S) puis f(S) et de savoir construire sur les gènes des opérateurs de croisement et de mutation qui donnent comme résultats des solutions (réalisables ou pas) du problème considéré.
Comme le nombre de gènes et la valeur des allèles dépendent du problème à résoudre, nous considérons des familles possibles de valeurs pour les allèles dans la partie suivante, puis des problèmes particuliers dans la dernière partie.





