Une autre idée pour résoudre le problème serait, partant d'une solution admissible correspondant à un point extrême du polyèdre, de chercher à augmenter la fonction économique sur un point extrême voisin pour un problème de maximisation, et ainsi, de proche en proche sur le polyèdre, arriver à un point optimal, la convergence est assurée quand le polyèdre est non vide et borné. L'opération consistant à passer d'un sommet à un sommet adjacent s'appelle un pivotage. C'est la traduction algébrique de ce principe qui est à la base de l'Algorithme du SIMPLEXE du à G. B. DANTZIG.
Tout le problème sera donc de caractériser les points extrêmes, de passer d'un point extrême à l'un de ses voisins et reconnaître le point optimal, et ceci de façon algébrique.
Pour appliquer l'algorithme du simplexe on met le problème sous Forme Standard : on transforme les inégalités en égalités en introduisant des variables d'écart toutes positives. Illustrons cela sur notre premier exemple :
Rappel : Programme linéaire du problème de production
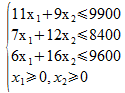
Exemple : Exemple d'écriture sous Forme standard
Dans cet exemple, il faut introduire trois variables d'écart y1, y2 et y3, toutes positives, représentant les différences entre les temps maximum d'utilisation des machines et leurs utilisations dans une solution admissible.
On a alors le problème ci-dessous que nous noterons PLFS :
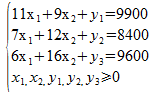
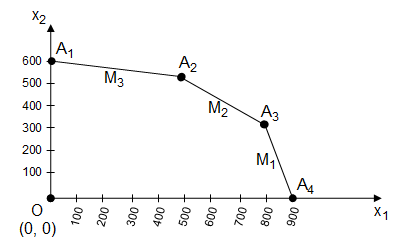
La question est de caractériser algébriquement les points extrêmes du polygone solution. Remarquons que, dans l'exemple, nous avons un système de 3 équations à 5 inconnus. Un tel système admet une infinité de solutions ou bien aucune. Si on donne à 2 des 5 variables la valeur 0, le système résultant, comprenant 3 équations et 3 variables, ou bien admet une seule solution ou bien n'en admet aucune. Il existe 10 façons de choisir 3 variables parmi 5. En allant de x1 = x2 = 0 à y2 = y3 = 0, nous obtenons respectivement les solutions : (x1, x2, y1, y2, y3) = (0, 0, 9 900, 8 400, 9 600) (solution admissible de départ), (0, 1 100, 0, - 4 800, -8 000), (0, 700, 3 600, 0, - 3 700), (0, 600, 4 500, 1 200, 0), (900, 0, 0, 2 100, 4 200), (1 200, 0, - 3 300, 0, 2 400), (1 600, 0, - 7 700, - 2 800, 0), (14 300/23, 7 700/23, 0, 0, 11 200/23), (36 000/61, 23 100/61, 0, - 16 800/61, 0) et (480, 420, 840, 0, 0). Seuls les première, quatrième, cinquième, huitième et dixième solutions correspondent à un point extrémal, ce sont respectivement O, A1, A4, A3 et A2, et nous les avons tous. Remarquons que les autres solutions ne sont pas admissibles, elles sont extérieures au polygone des contraintes, elles comportent des valeurs strictement négatives.
Définition :
De façon générale, si (x1, ..., xn, y1, ..., ym) est une solution des m équations, on dira qu'il s'agit d'une solution de base si au moins n de ses coordonnées sont égales à 0. Une solution de base dont toutes les coordonnées sont positives ou nulles est dite solution de base admissible. On peut alors démontrer :
Théorème 1
Si (x1, ..., xn, y1, ..., ym) est une solution de base admissible de PLFS alors (x1, ..., xn) est un point extrême de PLFC. De plus tout point extrême du problème s'obtient de cette façon d'une solution de base de PLFS/
Théorème 2
Si PLFS admet une solution optimale, il existe une solution de base admissible qui est solution optimale de PLFS
La résolution de PLFC peut donc se faire en examinant les solutions de base admissibles de PLFS, dont le nombre est borné par 
. Mais cette méthode est peu réaliste car il peut y avoir un nombre exponentiel de cas à tester. L'algorithme du simplexe permet de résoudre PLFC en examinant un nombre de solutions de base qui, sauf exceptions, est relativement petit. Empiriquement, le nombre d'itérations se situe entre 1,5m et 2m.