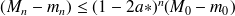Théorème fondamental pour les chaînes régulières
Méthode :
On considère une chaîne régulière (E fini). Elle possède alors une et une seule loi de probabilité invariante. Notons la
.
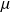Celle ci vérifie :
a)
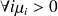
b)
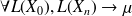
c)
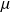est l'unique solution de
.
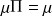
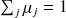Complément :
Soit A une matrice stochastique (carrée
,
,
)
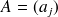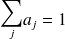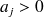On suppose que
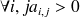
Soit
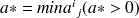
Soit
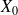un vecteur colonne
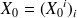et par récurrence
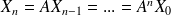
Posons
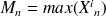et
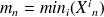
alors :
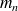croissante et
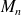décroissante et elles convergent vers la même limite et
