Analogie avec les chaînes régulières
Méthode :
Soit C une classe finale de période d. Il existe une unique loi de probabilité invariante sur cette classe. Notons la
.
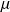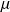vérifie :
a)
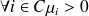
b)
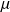est l'unique solution de :
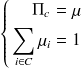
où
est la matrice
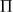restreinte à
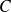
c) Si
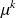est la loi invariante de la chaîne
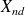reistreinte à
(
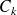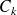la chaîne cyclique) alors :
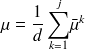
En particulier, chaque sous classes cycliques
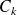de C à la probabilité
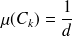
Expliquons un peu ce théorème. Par exemple, C est une des classes finales de la chaîne sur E.
Elle est de période d, elle a donc d sous-classes cycliques :
.
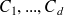Elle parcourera donc dans le même ordre et successivement ses d sous classes cycliques.
